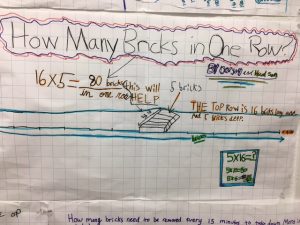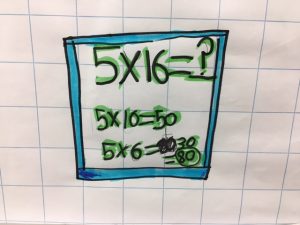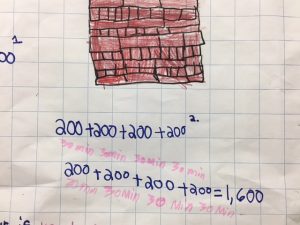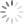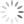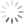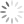Making Math Relevant

Simply providing a context to mathematics does not ensure that students will find the task relevant or engaging. Students can be drawn to a problem because it relates to their lives in a real way, or there may be something interesting about a task that intrigues them and challenges them to think deeply.  Mathematics that relate to other areas the student is currently studying can also provide relevance. Sometimes it’s not a matter of what specific problem is given, but how it’s posed by the teacher that piques students’ curiosity and results in deep engagement.


Where’s the Math in the MURO Wall?

  By drawlins • November 9, 2017 , ,

 Fourth Graders Participated in a Political Art Installation, and then Posed Mathematical Questions About It.  

 “It’s my first political performance and I just felt I had to do it now. I wanted to show that any wall is dismantlable. We, the public, can tear down walls when society gets together. It could be a mental, physical, or political wall – the point is, it’s ephemeral.”–Bosco Sodi, Artist

Photos by Robert Banat:   RobertBanat.com  RobertBanat@gmail.com

Here Are the Range of Math Questions They Asked:

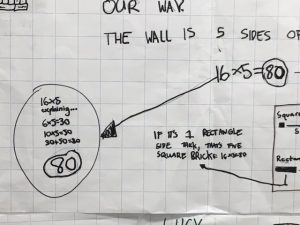
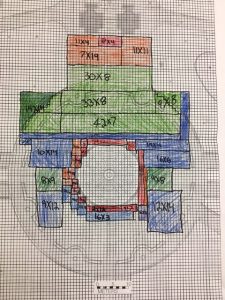
How Can We Use the Size of One Brick to Determine the Height and Length of the Wall?

How Many Inches Taller Is the Wall Height Compared to the Average Height of a 4th Grader? 

 

How Many Bricks Are in Each Layer?

 

 

Does Each Row Have the Same Number of Bricks?

 

 

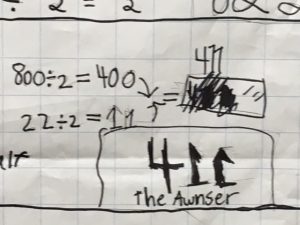
If Muro is Dismantled in 4 Hours, How Many Bricks Are Taken Down in 15 Minutes?

 

 

 

 

 

 

 

 

If There Were 20 People on Each Side of the Wall Taking Down 1 Brick Each, How Many Bricks Would Each Person Take Down?

 

 

How Many Bricks Could 8 People Remove During Each Hour If They Worked All Three Hours?

 

How Many Bricks In One Row?

 

 

How Many Bricks Need to be Removed Every 15 Minutes to Take Down Muro in Four Hours?

 

 

 

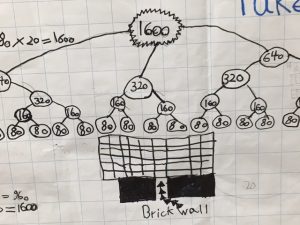
How Can Two Lines of People Dismantle 1,600 Bricks?

 

How Many Bricks Are Going Horizontally?

 

 

1,644 Bricks Were Dismantled in 4 Hours. How Many Bricks Were Dismantled in One Hour?

 

 

How Many Bricks Are There In Every Other Row Starting From the Top?

 

 

How Tall Are We Compared To The Muro Wall?

 

 

How Can 80 Volunteers Dismantle Muro?

 

 

Six Scenarios To Take Down Muro in Four Hours

 

 

There Are 1,644 Bricks. How Many Bricks Would Each Person Remove?

 

Is The Longest Block Area Also The Biggest?

  By drawlins • June 9, 2017 , , ,

Blog entry by Ariane Stern & Julie Kim

 

First Graders Explore Area and Perimeter

Earlier in the year, we introduced the concept of area—that you can measure how small or large a space is. After measuring various shapes with non-standard units (e.g. tiles, beans, paperclips), first graders developed an understanding that with bigger units like popsicle sticks, you’d need fewer of them to cover a certain area and that you would need many more small units like beans to fill that same area. Later in the  year, we began a unit on linear measurement. Again, we used manipulatives to measure the length of objects. This time, we focused  on ways to accurately measure length, such as figuring out which side is the length, and measuring by starting at the edge. After learning how to measure length accurately with one unit, we moved again to the idea of measuring the same object with different sized units. Once again, it takes less popsicle sticks to measure the length of a book, and more cubes, if you were measuring the same length.

 This year, to culminate our study on linear measurement, we challenged first graders to measure how long each Lower School classroom’s block area is. In small groups, first graders went to each classroom, calculated which side was the longest side and measured it with string. They brought their strings back to our classroom and proceeded to measure how long they were with popsicle sticks, tiles, and double unit wooden blocks. Afterwards, we collected each group’s data and compared the number of double unit blocks it took to measure the length of each string. We put the lengths in order to see which block area was the longest.

Along the way, we ran into some problems, just as mathematicians do in real life! What would we do if the double units were too long or too short for the end of the string? That led us into a conversation about fractions. We looked at halves, quarters, and thirds of rectangles and also looked at circles to deepen our understanding of fractions. This helped some groups to make more accurate measurements.

 

Then, Julie showed the class some pictures. Tasha’s block area was the longest, but it was very narrow and skinny. Diane’s block area was the shortest, but it was very wide. We wondered, just because a block area is the longest, does that mean it’s the biggest?

What a big question!

How would we figure that out? We knew what all the lengths of the block areas were, but how would we figure out how big they were? What were we even looking for? One student shouted, “The area! How were we going to figure out the area? We drew a rectangle on the board, showing how we knew the lengths. What else would we need to know to find the area? This was a puzzle. But calling upon what we had already learned about area, we realized that we needed to know the width of each block area. Wow!

Each group then went back to their assigned classroom, this time measuring the width of each block area. When they came back, they measured their new strings again with double unit wooden blocks. Then they used graph paper to replicate their block area. Each square of the graph paper represented one double unit block. Then they counted all the squares to figure out the area. This was hard work! Many of the shapes they drew had over 100 squares! Each group had to count the squares in their shape multiple times to try and get the most accurate count.

At the end of the day, we did figure out which classroom had the largest block area.

It wasn’t the longest block area!

Controversial Crowd Counting at Washington Square Park

  By drawlins • June 2, 2017 , ,

Estimating Protest Crowd Size Using the Jacob’s Method of Crowd Counting.

“For many events, especially political rallies or protests, the number of people in a crowd carries political significance and count results are controversial”- Wikipedia

 “Almost everyone who has tried to make a crowd estimate has a vested interest in what the outcome of the estimate is”– Charles Seife, Professor of Journalism and Mathematician at NYU.

Fourth graders applied the Jacob’s method of crowd counting to estimate the protest crowd that gathered in Washington Square Park on Wednesday, January 25th, 2017. The emergency rally was organized in response to President Trump’s executive order implementing a ban on immigrants entering the country from large Muslim populations, including Iran, Iraq, Libya, Somalia, Sudan, Syria, and Yemen.

Getting the Numbers Right: The Jacobs Method of Crowd Counting

Herbert Jacobs, a University of California journalism professor in the 1960’s, devised a basic density rule that has been widely accepted. Watching students protesting the Vietnam War from his office window, Jacobs saw that had gathered on a plaza that was arranged in a grid. He counted those in a few squares to get an average number per square and multiplied that by the total number of squares. He also came up with a basic density rule that states a “light crowd” has one person per square meter, and doubled that for a “dense crowd”. A “heavy crowd” would have as many as four people per square meter, according to this method.

Using People Per Square Meter as Density Factors to Determine Crowd Size.

One person per square meter 

Three people per square meter

 

 

 

 

 

 

 

 

 

 

 

Nine people per square meter

Six people per square meter

Students Estimated Densities by Using an Aerial View of the Protest Crowd, a Scale Diagram of the Park, and Multiplication.

Washington Square Park Diagram Showing Density Arrays.

Six people per square meter density computation

Nine people per square meter computation

Making Sense of Problems by Seeing How They are Structured.

  By drawlins • June 1, 2017 , ,

 Kindergartners Use Dramatic Play to Model the Structure of Addition and Subtraction Problems.

Kindergartners related math stories to birds, their current social studies and science topic, by using dramatic play to act out addition and subtraction problems. Through these stories, students explored the action in different structures of problems (see chart below). Some examples of addition structure bird stories that students acted out were result unknown, change unknown, and both addends unknown. “Students who are taught to approach problems by looking at their structures through the use of a visual model are more likely to perform better than students who do not” (NCTM, 2014, pg. 50). This approach helps students make better sense of the action that is happening in problems and rely less on using keywords that can often be interpreted in many different ways (Karp, 2014, pg. 21).

An Example of Student Work Showing Change Unknown Structure Along With a Structure Diagram:

“Six pigeons were pecking on the sidewalk on Bleecker Street. Some more pigeons came to see what they were pecking at. Then there were ten pigeons.” (CHANGE UNKNOWN/ADD TO). 

Addition/Subtraction Problem Structures:

2014 Karp, Karen S., Teaching Children Mathematics. National Council of Teachers of Mathematics

2014 NCTM. Putting Essential Understanding of Addition and Subtraction into Practice

From Cooking to Counting

  By drawlins • May 9, 2017 , ,

First Graders Cook, Question, and Count

By Julie Kim, First Grade Associate teacher

In the real world, we confront daily math problems through a process of noticing and wondering. After our mind has determined a question about a scenario, whether it is counting how many more blocks you need to walk or how many servings to cook for dinner, we proceed to the next step: plan, search, and gather. We plan for what steps we are going to take in order to answer the question. We search for the separate variables and pieces of information that we need in order to solve the question. We gather these pieces of information then puzzle them up in a way that will help us solve the problem. Will we, as mathematicians, get the answer we are looking for the first time around? Not always. Will we get an answer immediately? Not guaranteed. Will we persevere and try over and over again until we do? We should. Through real world work, first graders develop stamina and perseverance as they attack the challenges and questions that they are eager to solve. This is where the real work happens.

Continue reading

The Math Relationship of Blocks

  By drawlins • February 26, 2017 , , ,

What can a student in the fours do when they run out of a certain sized block? 

They can use the “recipe” or conversion chart they made to create the block size they need from other blocks.

Students in Pre-K used classroom blocks to estimate, and then test, how many of each of the same size smaller blocks it would take to cover one double unit block. The class worked in pairs on this investigation, and then the class created posters of their mathematical conversions. They have found this conversion chart, or “recipe” useful to refer to when they run out of a certain block size because they can now create the size they need by combining (composing) other blocks. Continue reading

Cooking Up Arrays

  By drawlins • January 31, 2017 , ,

Do multiplication arrays need to be introduced as a ready-made convention, or can they be “constructed” by children using concrete objects while engaged in an open-ended task?

(An action research collaborative effort by second grade lead teachers, Tasha Hernandez, Bill Miller, and Lower School Math Coordinator, Debra Rawlins)

We began this project as a way to build math relevance into the annual second grade canned food drive. The students visit Saint John’s Food Pantry and spend a morning learning about the needs of the community. Then they pitch in and help out the staff for a few hours. When they return to school, they create signs advertising the canned food drive, and place collection boxes at various locations around the school.

Continue reading

Math, Push Carts, & City Hall Protest in New York

  By drawlins • February 24, 2016 , ,

Math with Social Justice Relevance

food samplingIt was a chilly day in January.

Fourth grade students and teachers went downtown to walk the streets of the busy financial district to meet food cart vendors. They were able to observe the variety of international selections that vendors were selling, and sample the delicious-smelling food.

Over 90% of the food vendors in New York City are first generation, or recent immigrants. This field trip gave students the opportunity to talk directly to the people who stood inside these carts, cooking food that reflected the cuisine of their home countries. Students were curious to hear the stories of where they immigrated from, and how they happened to enter into the business of selling food on the street. Continue reading