Monthly Archives: June 2017

Is The Longest Block Area Also The Biggest?

  By drawlins • June 9, 2017 , , ,

Blog entry by Ariane Stern & Julie Kim

 

First Graders Explore Area and Perimeter

Earlier in the year, we introduced the concept of area—that you can measure how small or large a space is. After measuring various shapes with non-standard units (e.g. tiles, beans, paperclips), first graders developed an understanding that with bigger units like popsicle sticks, you’d need fewer of them to cover a certain area and that you would need many more small units like beans to fill that same area. Later in the  year, we began a unit on linear measurement. Again, we used manipulatives to measure the length of objects. This time, we focused  on ways to accurately measure length, such as figuring out which side is the length, and measuring by starting at the edge. After learning how to measure length accurately with one unit, we moved again to the idea of measuring the same object with different sized units. Once again, it takes less popsicle sticks to measure the length of a book, and more cubes, if you were measuring the same length.

 This year, to culminate our study on linear measurement, we challenged first graders to measure how long each Lower School classroom’s block area is. In small groups, first graders went to each classroom, calculated which side was the longest side and measured it with string. They brought their strings back to our classroom and proceeded to measure how long they were with popsicle sticks, tiles, and double unit wooden blocks. Afterwards, we collected each group’s data and compared the number of double unit blocks it took to measure the length of each string. We put the lengths in order to see which block area was the longest.

Along the way, we ran into some problems, just as mathematicians do in real life! What would we do if the double units were too long or too short for the end of the string? That led us into a conversation about fractions. We looked at halves, quarters, and thirds of rectangles and also looked at circles to deepen our understanding of fractions. This helped some groups to make more accurate measurements.

 

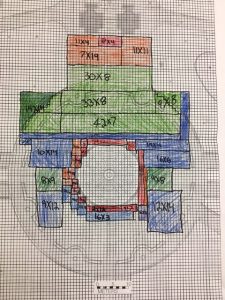
Then, Julie showed the class some pictures. Tasha’s block area was the longest, but it was very narrow and skinny. Diane’s block area was the shortest, but it was very wide. We wondered, just because a block area is the longest, does that mean it’s the biggest?

What a big question!

How would we figure that out? We knew what all the lengths of the block areas were, but how would we figure out how big they were? What were we even looking for? One student shouted, “The area! How were we going to figure out the area? We drew a rectangle on the board, showing how we knew the lengths. What else would we need to know to find the area? This was a puzzle. But calling upon what we had already learned about area, we realized that we needed to know the width of each block area. Wow!

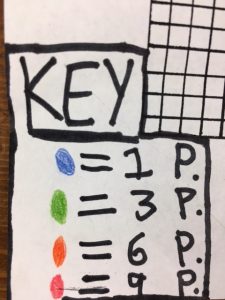
Each group then went back to their assigned classroom, this time measuring the width of each block area. When they came back, they measured their new strings again with double unit wooden blocks. Then they used graph paper to replicate their block area. Each square of the graph paper represented one double unit block. Then they counted all the squares to figure out the area. This was hard work! Many of the shapes they drew had over 100 squares! Each group had to count the squares in their shape multiple times to try and get the most accurate count.

At the end of the day, we did figure out which classroom had the largest block area.

It wasn’t the longest block area!

Controversial Crowd Counting at Washington Square Park

  By drawlins • June 2, 2017 , ,

Estimating Protest Crowd Size Using the Jacob’s Method of Crowd Counting.

“For many events, especially political rallies or protests, the number of people in a crowd carries political significance and count results are controversial”- Wikipedia

 “Almost everyone who has tried to make a crowd estimate has a vested interest in what the outcome of the estimate is”– Charles Seife, Professor of Journalism and Mathematician at NYU.

Fourth graders applied the Jacob’s method of crowd counting to estimate the protest crowd that gathered in Washington Square Park on Wednesday, January 25th, 2017. The emergency rally was organized in response to President Trump’s executive order implementing a ban on immigrants entering the country from large Muslim populations, including Iran, Iraq, Libya, Somalia, Sudan, Syria, and Yemen.

Getting the Numbers Right: The Jacobs Method of Crowd Counting

Herbert Jacobs, a University of California journalism professor in the 1960’s, devised a basic density rule that has been widely accepted. Watching students protesting the Vietnam War from his office window, Jacobs saw that had gathered on a plaza that was arranged in a grid. He counted those in a few squares to get an average number per square and multiplied that by the total number of squares. He also came up with a basic density rule that states a “light crowd” has one person per square meter, and doubled that for a “dense crowd”. A “heavy crowd” would have as many as four people per square meter, according to this method.

Using People Per Square Meter as Density Factors to Determine Crowd Size.

One person per square meter 

Three people per square meter

 

 

 

 

 

 

 

 

 

 

 

Nine people per square meter

Six people per square meter

Students Estimated Densities by Using an Aerial View of the Protest Crowd, a Scale Diagram of the Park, and Multiplication.

Washington Square Park Diagram Showing Density Arrays.

Six people per square meter density computation

Nine people per square meter computation

Making Sense of Problems by Seeing How They are Structured.

  By drawlins • June 1, 2017 , ,

 Kindergartners Use Dramatic Play to Model the Structure of Addition and Subtraction Problems.

Kindergartners related math stories to birds, their current social studies and science topic, by using dramatic play to act out addition and subtraction problems. Through these stories, students explored the action in different structures of problems (see chart below). Some examples of addition structure bird stories that students acted out were result unknown, change unknown, and both addends unknown. “Students who are taught to approach problems by looking at their structures through the use of a visual model are more likely to perform better than students who do not” (NCTM, 2014, pg. 50). This approach helps students make better sense of the action that is happening in problems and rely less on using keywords that can often be interpreted in many different ways (Karp, 2014, pg. 21).

An Example of Student Work Showing Change Unknown Structure Along With a Structure Diagram:

“Six pigeons were pecking on the sidewalk on Bleecker Street. Some more pigeons came to see what they were pecking at. Then there were ten pigeons.” (CHANGE UNKNOWN/ADD TO). 

Addition/Subtraction Problem Structures:

2014 Karp, Karen S., Teaching Children Mathematics. National Council of Teachers of Mathematics

2014 NCTM. Putting Essential Understanding of Addition and Subtraction into Practice

How Many Ways Can We See Six Tiles?

  By drawlins • June 1, 2017 , ,

Laying the Foundation for Addition by Exploring Parts of Six. 

Kindergarten students decomposed the number six by placing square inch tiles into different arrangements and then recorded how they saw the arrangements using numbers. One of the goals of this problem was to help students understand that numbers can be decomposed (broken apart) in many ways. Developing an understanding of part-part-whole relationships is the first critical step to grasping the concepts of addition and subtraction, properties, and algorithms (NCTM, 2014, pg. 11). For example, in later years, decomposition (part-part-total understanding) of multi-digit numbers are used in place value concepts and the operations of addition/subtraction, multiplication/division by applying the various properties of commutative, associative, and distributive.

Differentiating Through an Open Problem:

How Many Ways Can Six Tiles Be Arranged?

Each child arranged tiles in as many ways as they could. This open problem was accessible to every student in the class, and at the same time provided differentiation because of the challenging open-ended nature of the problem (see below, the same problem given at the college level). The class came together and examined all of the possible ways of arranging six tiles “side-to-side, and corner-to-corner”. Through this exploration, the geometric concepts of congruence and transformations (flips, slides, turns), were introduced. The students found 20 ways to arrange six tiles.

Six Tiles Problem by Professor David Meredith:

Below is the same six tiles problem given to mathematics students at San Francisco State University by Professor Meredith, of the mathematics department. Prior to San Francisco State Univ., David was a professor at MIT, and a Woodrow Wilson Fellow. Meredith’s students found 35 distinct non-congruent ways to arrange six tiles.

2014 National Council of Teachers of Mathematics, Putting Essential Understanding of Addition and Subtraction into Practice.