How many Ways Can You Make 121 Using a Combination of These Blocks?

Students in second grade worked on this challenging open problem for several days using base ten blocks.

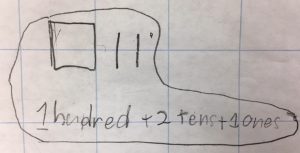
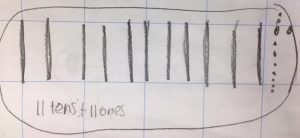
To understand place value deeply, students need to know that numbers can be represented more than one way. Through this problem, students explored the 10:1 base ten relationship and became flexible with decomposing hundreds, tens and ones many different ways. For example, in addition to representing 121 with 1 hundred, 2 tens, and 1 unit, students realized that 121 can be further decomposed into 12 tens and 1 unit cube, or 9 tens and 31 unit cubes.

This work provides a foundation for student strategies of breaking apart numbers by place to solve addition and subtraction problems, leading to a better understanding of the U.S. algorithm.

Student Examples- Can you find a Pattern?

As students worked on this problem, teachers challenged them to see if they could discover a pattern, and a systematic method of finding all of the possible ways to make 121. 

Taking the Problem Further:

The openness of this problem allows students to work on many different levels and some may notice that there is a pattern with the number of blocks used (the number increases by 9), as tens are systematically decomposed, as well as an alternating odd and even number of blocks.