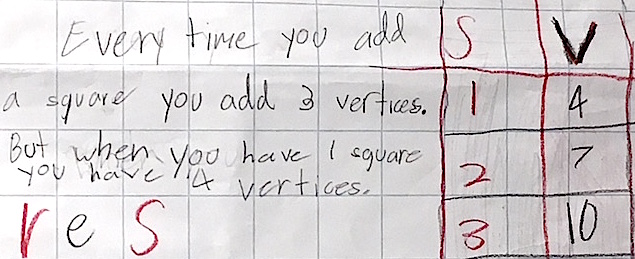The Squares and Vertices Problem
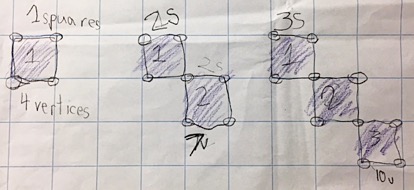
Students in third grade used one-inch square tiles to create a growing pattern by adding one additional tile to each consecutive pattern configuration. Tiles were placed vertex-to-vertex. Then students created a function table to record and analyze the relationship between the number of tiles and the number of vertices in their growing pattern. For example, in one pattern, for 2 tiles, there were 7 vertices, and for 3 tiles, there were 10 vertices, and so on. Students realized that once they recognized the abstract numerical pattern in their function charts, they could predict the growing pattern for any number of tiles without having to actually create further concrete models.
Functional thinking is an important entry point into algebra, and allows students to generalize and express relationships quantitatively. Natural language can be used to describe and express these relationships. Students were asked, “How would you describe the relationship between the number of squares and the number of vertices in your repeating pattern diagram?” Students compared various ways of describing their numerical relationships. We also analyzed the statement: “The number of vertices is equal to three times the number of squares, plus one” v = 3s + 1