Exploring Operations and Standard Algorithms

+ × ÷ –

Students dig deep into the operations and discover algebraic properties along the way.

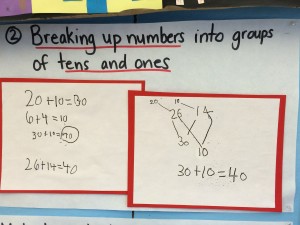
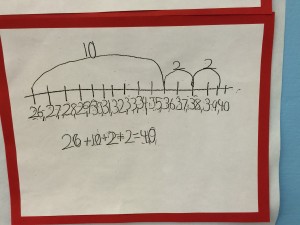
The goal is for students to build procedural fluency that is based on deep conceptual understanding. Fluency enables students to choose flexibly among methods and strategies to solve mathematical problems accurately and efficiently within a context. Through these early strategies, students learn how quantities can be taken apart (decomposed), and put back together in different ways. This lays the foundation for understanding the properties of the operations, and forms the basis of early algebraic thinking.

As students refine their methods for reliable algorithmic representations, we encourage then to adopt transparent models that they can understand, and explain to others. Above all, we stress that procedures never be used without deep conceptual understanding.