Project by: Neloy Kundu (12th Grade)
Project Advisor: Sergei Mikhelson
Student(s)’s Advisor(s): Sarvjit Singh Moonga
For my Honors Project, I studied material equivalent to a semester-long Multivariable Calculus college class. The reason I wanted to take on this Honors Project was to extend my knowledge of Mathematics in a meaningful way, especially because of my past experience into Calculus. In standard, single-variable Calculus, we study the relationship between one variable to a function. This in itself is important for studying the science of the real-word. Multivariable calculus effectively studies the relationship between multiple variables (as the name suggests) to a function.
While Single-Variable Calculus is useful for incorporating relationships between two things, in the real world, we often encounter multivariate problems. For instance, we can measure the relationship, between, say a country’s poverty rate and its relation to mortality rate, but this would not necessarily be a holistic view of the situation. This would be a single-variable approach. We should add more variables influencing the situation, like rate of disease, or increased criminality, and this is exactly how a multivariate system approaches the modeling of a function.
First, I learned about Vectors and Matrices. These are essential because vectors do not contain restrictions or rules on the number of dimensions we have. Effectively, we can model literally ANY DIMENSION through the use and generalization of vectors. Dimensions usually denote the number of variables and outputs, and having more in the case of multivariable functions is a MUST, because we live in a 3-d world – we cannot simply model every single problem graphically. But vectors allow us to at least describe (and investigate) each function.

Then, we learn to model functions not only on a coordinate plane, but in a vector-field or a contour sketch.
Next, I learned about partial derivatives (essentially measuring the impact an individual variable has to the output of the entire function) and what partial derivatives may entail in terms of curl, divergence, optimization, approximations, and other fancy mathematical things. 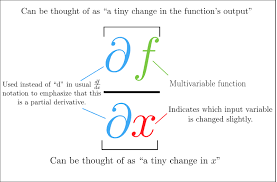
After this, I studied integrals in vector-valued functions, some of which studied were aimed at find the area under a line in as many dimensions as given. Then I studied multiple integrals and how they could measure area of surfaces and volumes. These integrals turned into cool theorems like Stoke’s , Greene’s, and the general Divergence theorem, which measure attributes of a function in a vector field, all of these having major implications physics and engineering, typically applied-math fields.
I have learned so much this past trimester and have really come to terms with my math knowledge and critical thinking ability, which I believe, has peaked heavily in terms of thinking away from conventional mathematics because this subject does challenge the student to envision new (and sometimes old) concepts in ways not conventional to past mathematics.


Approved